개발자의 스터디 노트
다층 퍼셉트론 본문
1. MLP(다층 퍼셉트론)는 기본적인 신경망 구성 요소입니다.

첫 번째 단계는 입력 벡터입니다. 입력 벡터를 첫 번째 Linear 층이 은닉 벡터(hidden vector)를 계산합니다. 이 벡터가 두 번째 표현 단계입니다. 입력과 출력 사이에 있는 은닉층의 출력을 은닉 벡터라고 부르고 은닉 벡터의 값은 층을 구성하는 각 퍼셉트론의 출력이라고 이해해도 됩니다. 두 번째 Linear 층은 은닉 벡터를 사용해 출력 벡터(output vector)를 계산합니다. 다중 분류에서는 출력 벡터의 크기가 클래스 개수와 같습니다. 위 그림에서는 은닉층이 하나지만 중간 단계는 여럿일 수 있습니다. 단계마다 각각의 은닉 벡터를 만듭니다. 최종 은닉 벡터는 항상 Linear 층과 비선형 함수를 사용하여 출력 벡터에 매핑됩니다. MLP의 강력한 성능은 두 번째 Linear 층을 추가하여 모델이 중간 표현을 학습할 수 있는 데서 비롯됩니다. 이 중간 표현은 선형적으로 구분할 수 있습니다. 즉 하나의 직선으로 데이터 포인트가 어느 쪽에 놓여있는지 구별할 수 있습니다. 분류 작업에서 선형으로 구분하기 같은 중간 표현의 학습은 신경망을 사용하여 얻은 중요한 결과이며 모델링 능력의 정수입니다.
2. 간단한 예:XOR

결정 경계에 의해 답을 구분하는 학습을 하였으나 아래쪽에 회색의 부분은 올바르게 분류하지 못하였습니다.

퍼셉트론에 비해 별과 원을 분류하는 결정 경계를 훨씬 정확하게 학습합니다.
그래프에 MLP 결정 경계가 두 개로 나타나 특별해 보이지만, 사실 하나의 결정 경계입니다. 중간 표현이 공간을 변형해 초평면 하나가 두 곳에 나타나도록 만들어서 결정 경계가 이렇게 보입니다.
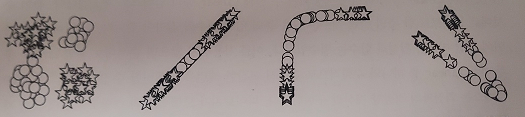
위 그림을 보면 왼쪽부터 신경망의 입력 > 첫 번째 층의 선형 출력 > 첫 번째 층의 활성화 함수 출력 > 두 번째 층의 선형 출력입니다.
첫 번째 층의 선형 출력은 별과 원을 그룹으로 모읍니다.
두 번째 층의 선형 출력은 선형적으로 구분할 수 있도록 데이터 포인트를 재조직합니다.
퍼셉트론은 추가 층이 없으므로 선형으로 구분되도록 데이터를 변형하지 못합니다.
3. 파이토치로 MLP 구현하기
우선 소스코드에서 사용할 패키지를 추가합니다.
import torch
import torch.nn as nn
import torch.nn.functional as F# MLP 클래스 생성
class MultilayerPerceptron(nn.Module):
def __init__(self, input_dim, hidden_dim, output_dim):
"""
매개변수 :
input_dim (int) : 입력 벡터 크기
hidden_dim (int) : 첫 번째 Linear 층의 출력 크기
output_dim (int) : 두 번째 Linear 층의 출력 크기
"""
super(MultilayerPerceptron, self).__init__()
self.fc1 = nn.Linear(input_dim, hidden_dim)
self.fc2 = nn.Linear(hidden_dim, output_dim)
def forward(self, x_in, apply_softmax=False):
"""
MLP의 정방향 계산
매개변수 :
x_in(torch.Tensor) : 입력 데이터 텐서
x_in.shape는 (batch, input_dim) 입니다.
apply_softmax (bool) : 소프트맥스 활성화 함수를 위한 플래그
크로스 엔트로피 손실을 사용
"""
intermediate = F.relu(self.fc1(x_in))
output = self.fc2(intermediate)
if apply_softmax:
output = F.softmax(output, dim=1)
return outputLinear층 2개 외에 렐루 활성화 함수가 첫 번째 Linear 층의 출력에 적용되어 두 번째 Linear 층의 입력으로 제공됩니다. 층이 순서대로 놓이므로 한 층의 출력 개수는 다음 층의 입력 개수와 같아야 합니다. 두 Linear 층 사이에 놓인 비선형 활성화 함수는 필수입니다. 이를 사용하지 않으면 Linear 층 두 개는 Linear 층 하나와 수학적으로 같아서 복잡한 패턴을 모델링할 수 없습니다. 이 MLP클래스는 역전파의 정방향 계산만 구합니다. 파이토치가 모델 정의와 정방향 계산에 맞춰 자동으로 역방향 계산과 그레이디언트 업데이트를 수행하기 때문입니다.
입력 차원의 크기는 3, 은닉 차원의 크기는 100, 출력 차원의 크기는 4인 MLP 객체를 생성합니다.
# MLP 객체 생성
batch_size = 2 # 한 번에 입력할 샘플 개수
input_dim = 3
hidden_dim = 100
output_dim = 4
# 모델 생성
mlp = MultilayerPerceptron(input_dim, hidden_dim, output_dim)
print(mlp)유닛 개수를 잘 정렬하여 차원이 3인 입력에서 차원이 4인 출력이 만들어짐을 보여줍니다.
MultilayerPerceptron(
(fc1): Linear(in_features=3, out_features=100, bias=True)
(fc2): Linear(in_features=100, out_features=4, bias=True)
)
랜덤한 2행(batch_size=2) 3열(input_dim=3)인 텐서를 생성합니다.
## 랜덤한 입력으로 MLP 테스트 하기
def describe(x):
print("타입: {}".format(x.type()))
print("크기: {}".format(x.shape))
print("값: \n{}".format(x))
x_input = torch.rand(batch_size, input_dim)
describe(x_input)타입: torch.FloatTensor
크기: torch.Size([2, 3])
값:
tensor([[0.5711, 0.7698, 0.7440],
[0.0934, 0.8351, 0.7767]])
2행 4열의 출력이 만들어지는 것을 확인할 수 있습니다.
y_output = mlp(x_input, apply_softmax=False)
describe(y_output)타입: torch.FloatTensor
크기: torch.Size([2, 4])
값:
tensor([[ 0.2076, 0.0890, 0.0468, -0.0130],
[ 0.1644, 0.0281, 0.0852, -0.0926]], grad_fn=<AddmmBackward0>)
파이토치 모델의 입력과 출력을 읽는 방법을 알아야 합니다. 앞 코드에서 MLP 모델의 출력은 행 2개와 열 4개가 있는 텐서입니다. 이 텐서의 행은 배치 차원에 해당합니다. 즉 미니 배치의 데이터 포인트 개수입니다. 열은 각 데이터 포인트에 대한 최종 특성 벡터입니다. 분류 등에서는 특성 벡터가 예측 벡터입니다.
예측 벡터란 확률 분포에 대응한다는 의미입니다. 훈련을 수행하는지 아니면 추론을 수행하는지에 따라 예측 벨터로 하는 일이 다릅니다. 예측 벡터를 확률로 바꾸려면 추가 단계가 필요합니다. 구체적으로는 벡터를 확률로 변환하는 소프트맥스 확성화 함수가 필요합니다.
# MLP 분류기로 확률 출력하기(apply_softmax = True)
y_output = mlp(x_input, apply_softmax=True)
describe(y_output)타입: torch.FloatTensor
크기: torch.Size([2, 4])
값:
tensor([[0.2824, 0.2508, 0.2404, 0.2265],
[0.2801, 0.2444, 0.2588, 0.2166]], grad_fn=<SoftmaxBackward0>)소프트맥스 함수는 기원이 여러 가지입니다. 물리학에서는 볼츠만 분포 또는 깁슨 분포로 알려져 있습니다. 통계학에서는 다항 로지스틱 회귀입니다. NLP에서는 최대 엔트로피 분류기로 알려졌습니다. 이 함수는 큰 양숫값이 높은 확률을 만들고 낮은 음숫값은 작은 확률을 만든다는 의미입니다.
MLP는 텐서를 다른 텐서로 매핑하는 Linear층을 쌓은 구조입니다. Linear 층 사이에 활성화 함수를 사용해 선형 관계를 깨고 모델이 벡터 공간을 비틀 수 있게 돕습니다. 이렇게 공간을 비튼 덕분에 클래스 사이를 선형적으로 구분해서 분류 작업을 할 수 있습니다. 또한 소프트맥스 함수를 사용해 MLP 출력을 확률로 해석할 수 있습니다. 하지만 특정 손실 함수를 사용하려면 소프트맥스 함수를 적용하지 말아야 합니다. 이런 손실 함수는 수학적으로 또 계산적으로 더 간단하게 구현되었기 때문입니다.
'파이썬 > 파이토치 자연어처리' 카테고리의 다른 글
| MLP로 성씨 분류하기 (2) : 학습 하기 (0) | 2022.02.19 |
|---|---|
| MLP로 성씨 분류하기 (1) : 학습 준비하기 (0) | 2022.02.18 |
| 옐프 리뷰 데이터셋으로 학습한 데이터 평가, 추론, 분석 하기 (0) | 2022.02.16 |
| 옐프 리뷰 데이터셋으로 학습 하기 (0) | 2022.02.15 |
| 옐프 리뷰 데이터셋으로 학습 준비하기 (0) | 2022.02.14 |
